Aluška.org: Věděním ke svobodě

V poslední době často narážíme na tématiku Zlatého řezu, nebo Fibonacciho posloupnosti v přírodě. Doposud však tyto pojmy nebyly dostatečně rozepsány a vysvětleny v žádném z článků. Proto jsem se rozhodla jednu charakteristiku zařadit pro ty, kterým doposud uniká přesný význam a důležitost těchto pojmů. Navíc se nám to bude hodit v dalším ze seriálů, které připravuji.

ZLATÝ ŘEZ

Zlatý řez (anglicky golden ratio, latinsky sectio aurea) je velmi zajímavá matematická konstanta, která lidstvo po staletí fascinuje svou všeobecností a harmonií. Zlatý řez je nejčastěji vnímán jako ideální poměr mezi dvěma úsečkami. Můžeme se setkat i s označením zlatý poměr, zlaté číslo nebo zlatá proporce.

Historie

Poměr založený na zlatém řezu údajně používali již Egypťané při stavbě pyramid. Rhindův papyrus (asi 1788-1580 př.n.l.) říká, že „V pyramidách je utajen tajemný kvocient nazvaný seqt“. Možná, že se jedná právě o zlatý řez. První písemné zmínky pak pocházejí z antiky od Eukleida (asi 340-287 př.n.l.), který ve svých Základech uvádí následující úlohu: „Rozdělte danou úsečku na dvě nestejné části tak, aby čtverec sestrojený nad větší částí měl stejný obsah jako pravoúhelník, jehož jedna strana má délku menší části a druhá má délku celé úsečky.“ Řešením této úlohy je právě rozdělení dané úsečky v poměru zlatého řezu.

O zlatém řezu pak dlouho neslyšíme a vrací se až v období renesance. Najdeme jej na obrazech (např. Poslední večeře od Leonarda da Vinci), v architektuře (chrám Notre-Dame v Paříži) a v designu (hudební nástroje). V tomto období se zlatému poměru daří dobře, protože mu tehdejší myslitelé přisuzují až božské vlastnosti. Ve 20. století se zlatému řezu věnoval například architekt a malíř Le Corbusier (1887-1965), který se snažil vytvořit univerzální proporční jednotku (viz. kniha Le Modulor, 1948).

Zlatý řez se nejčastěji značí řeckým písmenem ϕ (fí) na památku řeckého sochaře Feidia (asi 490-430 př.n.l.). Mezi jeho díly najdeme i sochu Dia Olympského, který byl považován za jeden ze sedmi divů světa. Podle některých zdrojů se však označení fí zavedlo spíše na počest Leonarda Pisánského zvaného Fibonacci (asi 1170-1240 n.l.). Jak uvidíme později, Fibonacciho posloupnost se zlatým řezem také úzce souvisí.

Výpočet hodnoty zlatého řezu

Představme si následující situaci:

rozdělení úsečky zlatým řezem

Úsečku délky a + b rozdělíme na dvě části a a b tak, aby byl poměr mezi celkovou délkou a + b a větší částí a stejný jako poměr větší částí a a menší části b. Když tento požadavek vyjádříme matematicky, dostaneme následující rovnici:

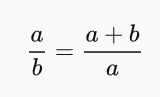
Tento poměr označíme jako zlatý řez.

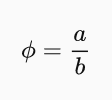
Úpravou výrazu vyjádříme délku a.

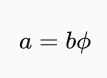
Dosazením do první rovnice získáme následující výraz:

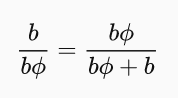
Nyní celou rovnici vykrátíme délkou b.

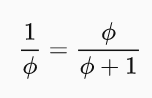
Rovnici zbavíme zlomků.

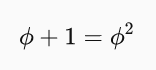
Převedením členů na jednu stranu získáme kvadratickou rovnici.

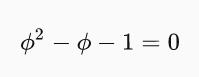
Rovnici vyřešíme a získáme hodnotu zlatého řezu. Protože jsme počítali poměr větší části k menší, musí poměr vyjít větší než jedna. Za hodnotu zlatého řezu tedy vezmeme řešení větší jedné, a to 1,618033…

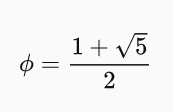
Hodnota zlatého řezu

Zlatý řez je číslo iracionální, nelze jej tedy zapsat konečným počtem číslic.

1,61803398874989484820458683436563811772030917980576286213544862270526046281…

Geometrická konstrukce zlatého řezu

Nyní se podíváme na možnost geometrické konstrukce zlatého řezu, která se nazývá Herónova.

Herónova konstrukce zlatého řezu

1. Sestrojíme úsečku AB, kterou chceme rozdělit zlatým řezem.
2. Z bodu B vztyčíme kolmici o délce poloviny |AB|.
3. Konec kolmice označíme jako bod C.
4. Sestrojíme trojúhelník ABC.
5. Sestrojíme kružnici n se středem v bodě C a poloměrem |BC|.
6. Průnik kružnice n a úsečky AC označíme jako bod N.
7. Sestrojíme kružnici m se středem v bodě A a poloměrem |AN|.
8. Průnik kružnice m a úsečky AB označíme jako bod M.
9. Délky úseček AB a AM jsou navzájem ve zlatém poměru.

Existují však i jiné metody geometrické konstrukce.

Geometrická konstrukce zlatého obdélníku

Zlatý obdélník je obdélník, jehož strany jsou v poměru zlatého řezu. Každý obdélník lze rozdělit na čtverec a další zlatý obdélník. Zlatý obdélník můžeme ze čtverce zkonstruovat takto:

konstrukce zlatého obdélníku

1. Sestrojíme čtverec ABCD, který chceme rozšířit na zlatý obdélník.
2. Úsečku AB prodloužíme na polopřímku.
3. V polovině úsečky AB sestrojíme bod D.
4. Sestrojíme kružnici k se středem D a poloměrem |CD|.
5. Průnik kružnice k a polopřímky AB označíme jako bod M.
6. Obdélník AMND je zlatý obdélníkem.
7. Délky úseček AM a MN jsou ve zlatém poměru.
8. Délky úseček AM a AB jsou ve zlatém poměru.

Zlatý řez kolem nás

ZLATÝ ŘEZ V PĚTIÚHELNÍKU

Pravidelný pětiúhelník jistě každý zná. Jedná se o pravidelný mnohoúhelník, takže všechny jeho strany a vnitřní úhly jsou shodné. Podobně jako ostatní mnohoúhelníky jej můžeme vepsat do kružnice a kružnici lze vepsat i do něj. Je to jediný pravidelný mnohoúhelník, který má stejný počet úhlopříček a stran. Můžeme jej nakreslit jediným tahem, a to včetně úhlopříček.

S pravidelným pětiúhelníkem se můžeme setkat i při zavazování obyčejných tkaniček u bot. Pozorujte následující obrázek:

pětiúhelník při zavazování tkaniček

Zlatý řez se v pravidelném pětiúhelníku vyskytuje například zde:

• Průsečík dvou úhlopříček dělí každou z nich v poměru zlatého řezu.
• Poměr délek úhlopříčky a strany pětiúhelníku je zlatý.
• Sestrojíme-li všechny úhlopříčky pětiúhelníku, dostaneme pěticípou hvězdu, uvnitř které je opět pravidelný pětiúhelník. Potom poměr stran původního a nového pětiúhelníku je druhá mocnina zlatého čísla.

ZLATÝ ŘEZ V PŘÍRODĚ

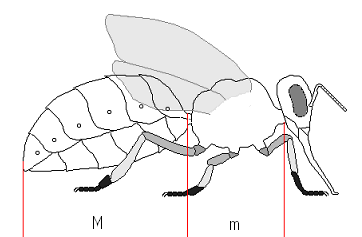
Se zlatým poměrem se setkáváme všude v přírodě, aniž bychom si to uvědomovali. Přijde nám totiž přirozený. Těla živočichů, rostlin, schránky mořských korýšů… tam všude můžeme zlatý poměr najít. Z nějakého důvodu se jím příroda „řídí“.

hlava kočky

lidská tvář

ZLATÝ ŘEZ V UMĚNÍ

Díky tomu, že známe zlatý poměr z přírody, vnímáme jej instinktivně jako krásný. Jsme na něj zkrátka zvyklí. Proto má zlatý řez široké využití v kompozici, designu, fotografii a architektuře. Umělci zlatý řez používají často i neúmyslně.

Leonardo da Vinci: Dáma s hranostajem

Leonardo da Vinci: Poslední večeře

ZLATÝ ŘEZ V ARCHITEKTUŘE

Zlaté číslo se již velmi dlouho používá v architektuře. Proporce ve zlatém poměru můžeme najít téměř ve všech významných stavbách po celém světě. Využívá se například základny ve tvaru zlatého obdélníku, okna a dveře se rozmisťuji dle zlatého poměru, apod.

Taj Mahal

Akropolis

Fibonacciho posloupnost

Fibonnaciho posloupnost je definována takto:

F₀=1

F₁=1

F_n=F_n-1+F_n-2

První dva členy posloupnosti jsou rovny jedné a každý další člen je roven součtu dvou předchozích členů. Uvedu začátek řady: 1, 1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13…

Podobně jako zlatý řez, i Fibonacciho řadu lze najít v přírodě. Podívejme se třeba na počty okvětních kvítků: 3 (lilie, kosatec), 5 (pryskyřičník, karafiát), 8(stračka), 13 (blatouch). Květiny své listy také často rozmisťují ve zlatých spirálách, což prý souvisí s optimálním zachycením dopadajícího světla.

Nyní zkusme spočítat několik poměrů dvou za sebou následujících členů Fibonacciho posloupnosti:

• 1/1 = 1
• 2/1 = 2
• 3/2 = 1,5
• 5/3 = 1,666…
• 8/5 = 1,6
• 13/8 = 1,625
• 21/13 = 1,615…
• atd.

Všimněte si, že poměr dvou následujících členů Fibonacciho posloupnosti konverguje k hodnotě zlatého řezu. Toto tvrzení zde nebudu dokazovat, uvádím ho pouze pro zajímavost.

použité zdroje:

http://www.volny.cz/zlaty.rez/diplomka.html

Vlasta Chmelíková: Zlatý řez (bakalářská práce, MFF UK, 2006)

http://voho.eu/wiki/zlaty-rez/